Bild 3

Bild 4

Bild 5

Bild 6

Bild 7

Bild 8

Bild 9

Bild 10

Bild 11

Bild 12

Bild 13

Fraktale aus Polynomen

Bisher veröffentlichte fraktale Motive beruhen auf Varianten zufällig gefundener Rekursionsgleichungen oder entsprechen Fixpunkt-Lösungen ohne Bifurkationen (Lösungsaufspaltungen). Das hier geschilderte Verfahren ist neu, ebenso die Art der Bilder. Es kann jede Komplexe Funktion f(z) = 0 benutzt werden, die ein eindeutiges f'(z) besitzt.

Mathematische Methode mit Beispielen
Ein bekanntes Fraktal
Jedes beliebige Polynom f(z) = 0 kann durch Iteration mit dem Newton-Verfahren

gelöst werden, auch wenn z = x + iy eine komplexe Größe ist. Bei Mehrfachlösungen hängt das konkrete Einzugsgebiet (als Farbe im Bild) von der Wahl der Anfangswerte x_a und y_a ab (Koordinaten eines Bildpunktes). Für die drei Fixpunkte der Gleichung

ergibt sich das bekannte Fraktal, an dessen Linien immer alle drei Gebiete aneinanderstoßen. Nennen wir es den dreizackigen "Einfachstern".

Dimensionserweiterung
Setzt man jetzt für z eine bestimmte hyperkomplexe Zahl ein (siehe Tafel 1) und löst (**) mit (*) für alle Komponenten von z, dann ergibt sich mit dem Ansatz (1) ein "Doppelstern" (6zackig) aus 9 Farben, mit dem Ansatz (2) ein "Dreifachstern" mit 27 Farben (Bild 13). Die hyperkomplexen Definitionen Quaternion (doppeltkomplexe Zahl) oder Oktave (doppeltes Quaternion) /3/ verändern den Einfachstern im Prinzip nicht und führen auch nicht zu dem im nächsten Abschnitt beschriebenen Effekt. Wohl aber Ansatz (3) und ähnliche Definitionen wie die Ansätze (4)–(6). Bei (3) ist zu beachten, daß die Anfangswerte der einzelnen Komponenten niemals gleich sein dürfen.

Rückprojektion durch Einschränkung der Freiheitsgrade
Wenn nun Gleichung (*) in verstümmelter Form benutzt wird, indem man die Iteration einer oder mehrerer Variablen unterläßt, sie als Konstanten behandelt, entfernt man sich vom ehemaligen f(z). Man bearbeitet für jeden Bildpunkt nun eine zwar benachbarte, aber neue nichtlineare Gleichung, die im allgemeinen nicht mehr analytisch darstellbar ist. Das vorher durch (*) abgeschlossene (konservative) System des "Sterns" wird geöffnet, erhält Restriktionen durch das Nullsetzen oder Verändern von z. B. dp und dt (s. Kommentarklammern Zeile 60). Jeder Eingriff solcherart muß als Verlust bzw. Zuwachs bezeichnet werden, vergleichbar mit Dissipation.
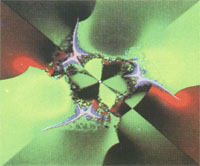
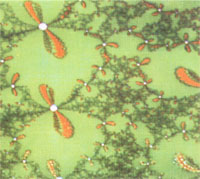
Es entstehen Bilder neuartiger Struktur. Für p und t um ±2 endet das Gebilde, während der Stern bis Unendlich reicht. Eine Entsprechung wäre das Mandelbrotsche Apfelmännchen, jedoch ohne Ähnlichkeiten. In der Nähe des Bildmittelpunktes bei sehr kleinen p,t-Werten entsteht der Einfachstern. Je mehr man nach außen wandert, desto "verbeulter" werden seine Glieder. Dann entstehen sprunghaft völlig neue Fraktale. Die alten Fixpunkte sind zerfallen, neue erschienen, und die Gebiete mit zyklischen Lösungen erinnern an "Wirbelsäulen" und "Insektenflügel". "Kakteenkugeln" mit blumiger Feinstruktur tauchen auf. Durch eine entsprechende Farbkodierung lassen sich somit Welten darstellen, die der lebendigen Welt nicht unähnlich sind. Bisher konnten nur wenige Proben aus dieser unentdeckten Vielfalt entnommen werden. Es bleibt dem Leser überlassen, das spannende Spiel fortzusetzen. Das Phänomen der Fraktale ist noch relativ ungeklärt. Falls man zufällig einen hyperkomplexen Ansatz findet, der für ein passendes f(z) am echtesten reale Objekte (z. B. Eisblumen, Schaum, Organismen) modelliert, sollten sowohl die Biologen als auch die Physiker nach Anwendungen dieser hyperkomplexen Größen Ausschau halten.

Rechentechnische Realisierung
Da die Bilder auf einem Robotron-BVS A 6472 visualisiert werden konnten, mußten sie optimal aus 512 x 512 Bildpunkten zu je 8 Bit bestehen. Mit einem speziellen Programm wurde aus etwa 200 Varianten die günstigste Farbtabelle gewählt, um die Grauwerte in Falschfarben darzustellen. Zum Rechnen der Bilder kamen SKR-Rechner zum Einsatz (SM4, SM14), wobei die Rechenzeiten zwischen 3 und 20 Stunden lagen. Übertragen wurden die fertigen Bilder per Magnetband, danach vom Farbmonitor abfotografiert mit einer Practica (Teleobjektiv, UT 18, 1/8 s).
Prinzipiell ist die Nutzung jedes mit PASCAL programmierbaren Computers möglich, wobei jedoch sehr lange Rechenzeiten auftreten können. In diesem Fall sind kleinere Bilder zu empfehlen (überall Austausch der Zahl 512). Die spätere Visualisierung muß gesondert an die vorhandene Technik angepaßt werden.

Programmbeschreibung
Unter Austausch der Zeilen 38–40, 47–61 und 84 wird das Programm (PASCAL, siehe Bild 1) auch zur bildmäßigen Simulation beliebiger dynamischer Systeme genutzt. Es kann dadurch für viele Anwendungszwecke brauchbar sein.

               Bild 1 Programm zu Bild 3                 Bild 2 Programmausschnitte für die Ansätze 2 und 3 
                                                                      Multiplikation der 6dimensionalen Arrays FM = KFxG

Bildkodierung
Es werden gleichzeitig zwei Bilder (A und B) zeilenweise auf Platte geschrieben (Zeile 89). Sie müssen zusammen betrachtet werden, wenn man das Lösungsverhalten auswerten will. Zur Kodierung stehen die Grauwerte 0 bis 225 zur Verfügung.
Im A-Bild wird für Fixpunkte als Grundfarbe der Quadrant abgebildet, in dem die Lösung liegt. Das hat den Nachteil, daß mehrere Attraktoren (Anziehungspunkte) im gleichen Quadranten nicht getrennt werden, und den Vorteil, das Nullwerden einer Komponente sehen zu können. Der Farbwechsel mit einer glatten Linie hat allerdings nichts mit den Fraktalen zu tun. Um zusätzlich die für eine vorgegebene Genauigkeit benötigte Iterationszahl abzubilden, wird auf den Grundgrauwert die Anzahl addiert (beschränkt bis 50). Nun sind alle Einzugsgebiete doch noch zu trennen, weil dort die Konvergenz stark fällt. Zufällig wurden auf diese Weise die "Netze" und "Flügel" sichtbar, die aus sehr schmalen Bifurkationen des Hintergrundes bestehen (kleiner 10^-6). Größere Bifurkationen kann das Programm trennen und konkret in Grauwerte des A-Bildes umsetzen. Da wäre Grauwert 22 ein Zweierzyklus, 23 ein Dreierzyklus usw. bis 35. 
Das B-Bild trennt exakt alle Attraktoren voneinander. Es sieht "sauberer" aus, berücksichtigt aber weder Konvergenz noch Bifurkationsverhalten. Man erkennt jetzt, zu welchem Attraktor die in Bild A herausgehobenen Zyklen gehören. Die Kodierung erfolgt durch asymmetrische Wichtung des letzten x-y-Paares (Zeile 84), um Fehler bei häufigen symmetrischen Lösungen auszuschalten. Für beide Bilder gleich markiert sind die Abbruchbedingungen bei Divergenz, Division durch Null und Überschreiten von 400 Iterationen.

Eingaben
Wegen der relativ langen Rechenzeiten erwies es sich als günstig, das Bild abschnittsweise zu erzeugen, d. h. mehrmals denselben Task zu starten. Im Dialog gibt man zuerst die beiden File-Namen ein (z. B. H1.A bzw. H1.B), dann von welcher Zeile bis zu welcher Zeile gerechnet werden soll. Diesen Abschnitt teilt das Programm als Zwischensicherung in drei File-Versionen auf. Die fertigen Einzelteile lassen sich problemlos aneinanderhängen. Zufällig stimmt die Blocklänge der SKR-Rechner mit der Bild-Zeilenlänge überein (512 Byte), so daß die Blockzahl als Zeilenanzahl zu lesen ist. Dadurch kann man ohne Notizen bei der richtigen Zeile fortsetzen.
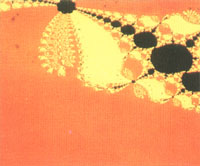
Um Eingabefehler zu vermeiden, sind die eigentlichen Bildparameter (siehe Tafel 2) im Programm zu ändern (Zeilen 3 bis 6 und 38). Zum Beispiel ergibt sich schon eine neue Gleichung durch Änderung der K-Komponenten (z³ + K = 0). Für neue quadratische Bildausschnitte ändert man die Parameter BREITE, VSX und VSY, die sich auf die Gesamtbildbreite und den neuen Bildmittelpunkt beziehen. 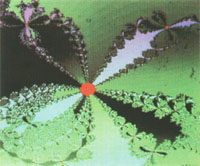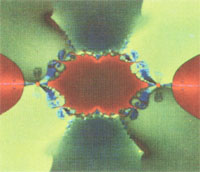Beispielsweise sind die Bilder 4 bis 6 Details des Bildes 3 und die Bilder 10 bis 12 Details des Bildes 9. Wenn man als Anfangswerte für alle x und y eine der drei Lösungen bei p = t = 0 wählt (Zeile 38), erhält das Gesamtbild eine Vierersymmetrie (Bild 9). Jede Veränderung dieser Anfangswerte bis hin zu punktweisen Neuzuweisungen, wie im abgedruckten Programm, erzeugt andere Ausgangsbilder ("Schnittebenen" der Funktion) mit neuartigen Details. Durch Beseitigen der Kommentarklammern bei Zeilen 53, 59, 60 und Einordnen der Zeilen 39, 40 nach Zeile 46 wird der Doppelstern berechnet.